上一篇,我们总结了个性化推荐系统中的经典算法——协同过滤算法中的相似度计算的相关性质,并给出了余弦相似度计算的示例。概括的说,协同过滤算法分为两类:
基于记忆的协同过滤算法和基于模型的协同过滤算法。相似度计算是归属于基于记忆的协同过滤算法之中用到的一个小分支,今天要讲解的矩阵分解模型(Matrix Factorization Model)却是属于基于模型的协同过滤算法的范畴。
内容概括:
1.引言
2.矩阵分解模型的数学表示
3.如何计算分解矩阵的元素——损失函数最小化
4.损失函数最小化的方法
1.引言
在推荐系统中,矩阵分解模型将用户和物品映射到一个共同的隐含因子空间R(该空间中向量的每一个维度代表一个隐含因子)。例如,在电影推荐中,用户的某个隐含因子可能代表用户喜欢动作类电影的程度,另外一个隐含因子可能代表用户的性格类型等;电影的隐含因子可能代表电影的类别(如动作、科幻)、电影适合的人群等。
2.矩阵分解模型的数学等式
如引言中所述,矩阵分解模型将用户和物品映射到一个共同的隐含因子空间,每一个用户和每一个物品都有自己的一些特性(隐含因子),用矩阵分解的方法可以从评分矩阵中分解出两个矩阵:用户-特征矩阵,物品-特征矩阵。
矩阵分解后,每位用户u被特征化为隐含因子向量Vu∈R,用来代表用户的喜好或兴趣;同理,每个物品i被特征化为隐含因子向量Vi∈R,用来描述物品的关键特征。矩阵分解模型的基本等式如下:
![]()
即,使用物品和用户隐含因子向量的点积来预测用户对物品的评分。
公式(1)的分解模型只考虑了用户和物品隐含因子对评分结果的影响,然而,在实际应用中,不同用户之间都有各自的评分偏差,例如用户u1习惯对喜欢的商品打4分,而用户u2习惯对喜欢的商品打5分;不同商品之间也有类似的情况,有的物品在大众用户中非常流行,而有的物品则只有少数特定用户群;除了用户和物品本身的偏差,不同的推荐系统所针对的领域数据也有各自的偏差,因此,公式(1)的一种变体为偏差矩阵分解,如下公式:
![]() 其中,W0是所有物品的平均评分,Wu是用户u对所有商品的一个偏置,Wi是i商品的偏置(偏置的概念其实上面已经简单的说明了,我们会在后续的LFM模型中具体介绍)。
其中,W0是所有物品的平均评分,Wu是用户u对所有商品的一个偏置,Wi是i商品的偏置(偏置的概念其实上面已经简单的说明了,我们会在后续的LFM模型中具体介绍)。
3.如何计算分解矩阵的元素
上述公式(2)是公式(1)的变体,实验表明(2)式在大多情况下也确实比(1)式的准确率要高,我们这里为了叙述的方便,就拿(1)式展开讨论。并且为了更直观的理解,将分解的向量分别用P,Q表示:即公式(1)等价于: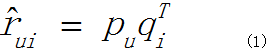
那么现在问题来了,我们最大的一个问题是,如何计算用户和物品各自的隐含因子向量pu和qi呢?如果我们能求出各自的pu和qi,再由上式,就可以得出用户u对物品i的一个预测评分(rui拔),进而根据评分大小对目标用户进行个性化推荐不就ok了吗,那么,该怎么求解pu,qi呢?
不要忘记了,我们还有实际的评分数据呢(Rui),那么我们就可以从实际评分(Rui)和预测评分(Rui拔)开始着手。我们的最终目标是为了尽可能准确的预测用户对一些没有打分的物品的评分,所以我们希望最小化实际评分与预测评分之间的差距,所以有如下公式(3):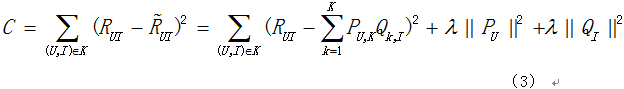
通常称上面的目标函数为损失函数,我们的目标即最小化损失函数。其中K为已知数据集中有实际评分的项;后面两个带有lambda的项是惩罚因子,目的为了防止数据过度拟合,且lambda是一个常数,可以通过实验获取。
4.损失函数最小化的方法
损失函数的最小化,可以通过两种方法进行求解——随机梯度下降法、交替最小二乘法。我们这里使用随机梯度下降法。
(1)首先分别对(3)式求P,Q的偏导数: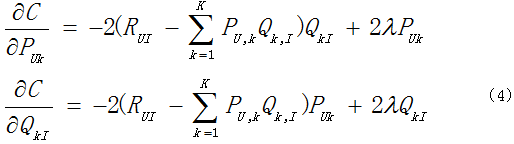
(2)分别令上式的偏导数等于0求得驻点之后,由随机梯度下降法可得下式: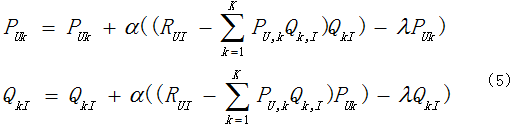
其中α是随机梯度下降的步长,是一个常数;lambda是惩罚因子项的一个常数。
利用上式对数据集进行训练,最终会求得用户-隐含因子矩阵P和物品-隐含因子矩阵Q,进而求得所有商品的预测评分。最后即可对目标用户进行个性化的商品推荐。
参考:Matrix Factorization Techniques for Recommender System——Yehusa Koren

男神,我仰慕你很久了。给个机会认识一下我呗?
是熊二吗?哈哈,宝宝又来逗我玩呢?